Das Jahr der Quantenphysik. Vor hundert Jahren, also 1925, entwarf Werner Heisenberg die Grundlagen der Quantentheorie (Jeden Sommer im Urlaub komme ich auf Helgoland an dem zugehörigen Gedenkstein vorbei). In PR 3334 hat Rüdiger Vaas sogar einen PR-Report diesem Jubiläum gewidmet. Ich dachte mir: Sollte nicht auch das WoC dieses Event würdig begehen? In unserer Lieblings-SF-Serie begeistert viele das Element des „sense of wonder“, die Anmutung von etwas Wunderbarem. Andere beschweren sich gar, wenn sie es vermissen. Quantenphysik leistet genau das: die Anmutung von Wunder. Was sie ebenso mit Hyperphysik gemeinsam hat wie die Tatsache, dass niemand sie wirklich versteht. Also, dies geht an die Kalups und Waringers unter euch (Ja, war’n Witz). Wie schon Niels Bohr sinngemäß bemerkte: Um das zu verstehen, muss einem schwindelig sein.

Mathematisch funktioniert Quantenphysik hervorragend. Die rechnerischen Vorhersagen sind perfekt, man darf nur nicht fragen, was dahintersteckt: „Shut up and calculate!“, Halt’s Maul und rechne – ein Zitat, das zu Richard Feynman passt, allerdings behauptet David Mermin, er wisse nicht mehr, ob er den Spruch selbst in die Welt gesetzt oder von Feynman geklaut habe.

Ich finde es höchst spannend, welche gedanklichen Klimmzüge und Verrenkungen schon angestellt wurden, um zu erklären, was hinter der Quantenphysik steckt. Praktischerweise hatte ich mal das Vergnügen, über das Buch „Conscious mind in the physical world“ von Euan Squires zu referieren, in dem es genau darum geht. Jüngst fiel mir das Manuskript wieder in die Hände. Es ist gespickt mit Differentialgleichungen, und ich habe drei Wochen gebraucht, um es wieder zu kapieren. Das tue ich euch natürlich nicht an. Aber ein bisschen schwindelig darf einem schon gern werden. Und deswegen gibt es trotzdem etwas Formelkram. Keine Panik, ich breche es auf die Mathematik eines Billig-Taschenrechners herunter: Nur Grundrechenarten. Wer Sudokus oder KenKens löst, dürfte auch damit keine Schwierigkeiten haben. Wem das auch noch zuviel ist, der kann die Rechnungen auch glauben und blättere weiter, bis wieder Prosa kommt. Also, bringen wir’s hinter uns:

Achtung, Mathe!

Für die Berechnungen, die ich euch zumuten (oder zumindest vorstellen) möchte, braucht ihr vor allem eins: die Multiplikation von Matrizen. Eine Matrix (nein, nicht die aus dem Kino) ist ein rechteckiges Zahlenschema. Also sowas wie ein Sudoku. Im Gegensatz dazu kann man Matrizen aber miteinander malnehmen. Man kann sie auch addieren und subtrahieren, aber das brauchen nicht mal.

Man multipliziert Matrizen, indem man die Elemente einer Zeile mit denen einer Spalte malnimmt und die Ergebnisse addiert. Im einfachsten Fall ist es nur eine Zeile (ein so genannter „Zeilenvektor“) und eine Spalte („Spaltenvektor“). Rechnet die Zahlenbeispiele mit, dann wird klar, wie es funktioniert. Andernfalls nehmt den Notausgang.

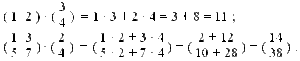
War’s schlimm? Hey, ich habe nicht gesagt, dass es Lustgefühle auslöst – aber es sollte sich verstehen lassen. Okay, dann kann’s ja jetzt losgehen. Folgt mir in den Kaninchenbau!

Die Schrödinger-Gleichung

Dies ist die Weltformel der Quantenphysik. Benannt ist sie nach Erwin Schrödinger (der auch der Namensgeber für die im Titel erwähnte Katze ist, auf die ich später noch komme), und sie lautet kurz: E = H . Darin sind E und H Operatoren. Operatoren? Ein Operator ist in der Mathematik ein hungriges Biest, das sich auf einen mathematischen Term stürzt, sobald es seiner habhaft wird, ihn frisst und dann einen neuen Term ausspuckt. Ein Beispiel aus dem Alltag (na ja) ist der Wurzeloperator: . Für sich allein ist er nutzlos, gebe man ihm aber ein Opfer, sagen wir eine 25, dann verschlingt er sie und macht eine 5 daraus: 25 = 5.

Im obigen ist E der „Energie-Operator“ und H der „Hamilton-Operator“. Dieser ist wiederum die Summe aus dem Operator T für die kinetische Energie (Bewegungsenergie) und V für die potentielle Energie (also praktisch das Kraftfeld, in dem sich das Objekt bewegt): H = T + V. Die ganze Aufgabe besteht darin, für ein gegebenes Kraftfeld V die Lösungen  (Psi) der Gleichung zu berechnen.  ist die „Zustandsfunktion“ und damit die mathematische Repräsentation des gerade betrachteten Quantenobjektes (Photon, Elektron, Atom, Molekül, Katze, Universum). Das ist nicht trivial; sobald der Verlauf des Kraftfeldes V einigermaßen anspruchsvoll ist, braucht man eine Menge Computer-Power, um die Lösungen zu finden.

Wenn man die Operatoren in der Schrödinger-Gleichung ausschreibt, sieht es furchtbar aus, deshalb lasse ich es bleiben. Soviel sei verraten: Es kommt darin h (Planck’sche Konstante) vor, woran man erkennt, dass es sich um Quantenphysik handelt. Und es kommt i = -1 darin vor, was darauf hindeutet, dass komplexe Zahlen eine Rolle spielen.

Aber ich will mit euch keine Atome berechnen. Um euch das Wesen der Quantenphysik zu erläutern, beschränke ich mich auf ganz einfache Dinge wie Elektronen oder Photonen. Ich übergehe auch die langen Ausführungen darüber, warum Licht aus Photonen besteht, das ist schon tausendmal erklärt worden; zumindest habt ihr euch schon längst daran gewöhnt. Und ich möchte euch die Wunder der Quantenphysik entfalten und nicht Gemeinplätze wiederholen, die auf jeder Semmeltüte stehen.

Also: Solange sich so ein Quantenobjekt fern von Kraftfeldern und anderen Widrigkeiten frei bewegt, kann man seine Zustandsfunktion  mit etwas gutem Willen grafisch darstellen: Als komplexe Funktion ist sie zweidimensional (x- und y-Achse), d.h. sie hat einen Realteil (Re) und einen Imaginärteil (Im) und erfordert dafür schon einmal eine ganze Fläche („komplexe Ebene“). Bleibt noch eine Dimension für die z-Achse übrig, das ist die Bewegungsrichtung des Objektes. Ein Elektron oder Photon, das sich in z-Richtung bewegt, sieht dann zu einem bestimmten Zeitpunkt etwa so aus wie in Bild 1:

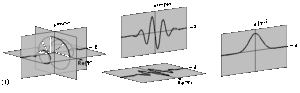
Linkes Bild: in voller Schönheit; mittleres Bild: Imaginärteil und Realteil einzeln (was Seitenansicht und Draufsicht des linken Bildes ist); rechtes Bild: Das „Betragsquadrat“ von . Ihr erkennt, dass das Ganze im weitesten Sinne eine Art Welle – präziser: ein „Wellenpaket“ – ist; und seine größte Schwingungsweite hat es dort, wo sich das Objekt vermutlich in etwa vielleicht so ungefähr befindet. Das Ganze sieht so ähnlich aus wie eine rotierende Matratzenfeder, denn die Schwingungen von Re() und Im() setzen sich zu einem um die z-Achse rotierenden Pfeil zusammen. Der Betrag || ist die Länge des Pfeils. Und das Betragsquadrat ||² (also die Länge des Pfeils mal sich selbst) ist das Einzige, das tatsächlich eine physikalische Bedeutung hat: Es ist die Wahrscheinlichkeit dafür, das Ding bei einer Messung zur Zeit t am Ort z anzutreffen. Alles andere ist nur ein (immerhin perfekt funktionierendes) mathematisches Modell. Und daher rotiert da in Wirklichkeit auch gar nichts (was auch immer Wirklichkeit sein mag), das stellt man sich nur so vor.

Die Besonderheit eines Quantenobjekts besteht also darin, dass es sich zu einer bestimmten Zeit eben nicht an einem bestimmten Ort befindet, sondern nur eine gewisse Wahrscheinlichkeit besteht, es dort zu finden. Diese Wahrscheinlichkeit lässt sich dann allerdings genau berechnen: ||². Die Schrödinger-Gleichung ist „deterministisch“, d.h. wenn man den Verlauf von  zu einem bestimmten Zeitpunkt kennt, kann man den Verlauf zu jedem früheren oder späteren Zeitpunkt daraus berechnen … bis man dem Objekt irgendwas in den Weg stellt, in das es reinknallt, z.B. bei Licht eine Fotoplatte. Ich bin da etwas altmodisch, heute nimmt man einen CCD-Sensor oder sowas, aber die gute alte Fotoplatte ist anschaulicher: Sie wird dort, wo das Photon reinknallt, geschwärzt. Und damit hat man plötzlich statt einer Wahrscheinlichkeit einen präzisen Ort. Das Wellenpaket ist dadurch allerdings zerstört worden. Und die ganze Krux der Quantenphysik ist, dass sie kein Werkzeug kennt, diesen Übergang vom Möglichen ins Faktische (die so genannte „Reduktion“ oder brutaler ausgedrückt: den „Kollaps“ der Zustandsfunktion) zu berechnen oder zu beschreiben. Davon handelt der ganze Rest.

Polarisiertes Licht

Zur Erläuterung dessen, was ich euch zeigen möchte, genügt es weitgehend, sich auf Lichtquanten (Photonen) zu beschränken, und dort auf die eine und einzige Eigenschaft der „Polarisation“. Fotografen kennen Polarisationsfilter, man benutzt sie, um störende Spiegelungen auszublenden. Auch manche Sonnenbrillen enthalten Polarisationsfilter. Sie lassen nur Licht durch, das in einer bestimmten Ebene schwingt, der Polarisationsrichtung. Da bei einer Reflexion das Licht ebenfalls polarisiert wird, kann man das reflektierte Licht mit einem Filter unterdrücken, das genau quer zu dieser Richtung steht.

Die Zustandsfunktion eines Lichtquants (unter Vernachlässigung aller anderen Eigenschaften wie z.B. der Farbe) ist dann ein Pfeil, der – quer zur Ausbreitungsrichtung z – die Polarisationsrichtung angibt. Also etwa so wie in Bild 2.

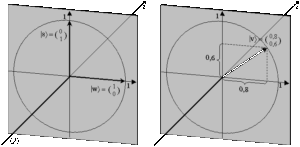
Achtung: Das ist nicht der rotierende Pfeil aus Bild 1. Dieser hier bedeutet eine konkrete Richtung im konkreten Raum, und auf den Polarisationsfiltern für Kameras ist diese Richtung mit einem kleinen Pfeil am Rand sogar markiert.

Der Zustand „waagerecht polarisiert“ wird durch die Zustandsfunktion |w beschrieben, der Zustand „senkrecht polarisiert“ durch die Zustandsfunktion |s, Bild 2 links. Zu den merkwürdigen spitzen Klammern komme ich gleich. Die Pfeile sind im mathematischen Sinne „Vektoren“ (Tatsächlich sind auch die -Funktionen in der Schrödinger-Gleichung – in einem sehr verallgemeinerten Sinn – Vektoren). Man beschreibt sie durch zwei Zahlen, die ihren waagerechten und ihren senkrechten Anteil darstellen. |w hat also den waagerechten Anteil 1 und den senkrechten Anteil 0, und umgekehrt bei |s. Das wird deutlicher, wenn wir schräg polarisiertes Licht |v betrachten (Bild 2 rechts). Warum heißt das Ding |v? Na ja, irgendwie muss es ja heißen. Das ist wie mit den Namen von Aliens in SF-Romanen. Es reicht, wenn der Autor sich etwas dabei gedacht hat. Oder auch nicht. Das schräg polarisierte Licht |v im Beispiel kann man sich aus 0,8 Anteilen waagerecht und 0,6 Anteilen senkrecht polarisierten Lichtes zusammengesetzt denken. Formal:

|v = 0,8 · |w + 0,6 · |s.

Es gibt natürlich auch andere schräge Polarisationsrichtungen. Ich nehme diese hier als Beispiel, weil die Zahlen nicht allzu krumm sind. Ein genau diagonal unter 45° polarisiertes Quant sähe so aus:

|d = ½ · |w + ½ · |s.

Aber Wurzeln sind keine Grundrechenarten, also Ihh-Bäh. Folglich versuche ich sie zu vermeiden, seid ihr da bei mir? (Jetzt sagt ihr vielleicht, was denkt der von uns? Nur das Beste, aber ich habe da schlechte Erfahrungen, außerdem hab ich’s versprochen.)

So, und was sollen also diese komischen spitzen Klammern? Nun, das ist eine auf Paul Dirac zurückgehende Schreibweise für Zustandsfunktionen. In der Schrödinger-Gleichung hätte danach statt  auch | stehen können, ich wollte euch nur nicht gleich erschrecken. Der Hintergrund ist, dass man Vektoren miteinander multiplizieren kann, allerdings kann man nur einen Zeilenvektor mit einem Spaltenvektor multiplizieren, wie weiter oben erläutert.

Dirac hat für Spaltenvektoren diese Schreibweise |a eingeführt und schreibt zur Unterscheidung den entsprechenden Zeilenvektor als a|. Beim Multiplizieren steht dann links eine spitze Klammer auf und rechts eine spitze Klammer zu, zum Beispiel a| · |b, abgekürzt auch a|b. Da eine Klammer auf Englisch „Bracket“ heißt, hat sich Dirac den Scherz erlaubt, das a| als einen Bra-Vektor und das |b als einen Ket-Vektor zu bezeichnen. Vielleicht, weil ihn der Hintersinn Bra = Büstenhalter amüsiert hat. O|O sieht ja in der Tat ein bisschen aus wie … damals war eben noch nicht alles politisch korrekt und #metoo gab’s auch noch nicht.

Was macht man nun mit diesem Produkt? Wenden wir es auf das schräg polarisierte Licht |v an, so erhalten wir

Und das ist das Betragsquadrat des Vektorpfeils, was nichts anderes ist als der Satz von Pythagoras in Bild 2 (rechts). Für |w oder |s dürft ihr es selbst nachrechnen. Das gilt übrigens auch für Schrödingers : | = ||², aber das nur am Rande.

Dinge, die man messen kann, heißen in der Quantenphysik „Observable“. Zu einer Messung gehört in der Welt der Quanten ein Operator, den man auf die Zustandfunktion anwendet, um ein Messergebnis zu produzieren. In unserer Welt der Vektoren ist ein Operator eine Matrix. Zum Beispiel misst man die senkrechte Polarisation von Licht mit einem senkrecht eingestellten Polarisationsfilter, und dazu gehört der Operator

Wenn man ihn auf unser schräg polarisiertes Licht |v loslässt, passiert folgendes:

Das senkrechte Polarisationsfilter erzeugt, wer hätte das gedacht, senkrecht polarisiertes Licht. Allerdings bleibt von |v nur dessen senkrechter Anteil übrig. Das eigentliche Messergebnis ist die Lichtintensität, die dabei zu erwarten ist, genannt der „Erwartungswert“ der Messung S, und geschrieben S. Achtung, man rechnet von rechts nach links:

Es sind demnach 36% der ursprünglichen Lichtintensität zu erwarten – oder anders: für ein einzelnes Photon des Zustandes |v beträgt die Wahrscheinlichkeit 36%, dass es durch das Filter hindurchkommt. Danach befindet es sich allerdings im Zustand |s, d.h. die Messung hat den Zustand verändert. Das ist ein wesentliches Charakteristikum der Quantenphysik. Die Messung verändert das Messobjekt und erzeugt („präpariert“) einen neuen Zustand. Merken!

Die Unbestimmtheitsrelation

Sie geht auf Werner Heisenberg zurück und ist auch als „Unschärferelation“ bekannt. Die Änderung des Messobjektes durch die Messung macht es bei manchen Eigenschaften unmöglich, sie simultan zu messen (Paradebeispiel: Ort q und Impuls p. Wenn euch „Impuls“ nichts sagt, denkt statt dessen an eine Geschwindigkeit, das trifft es nicht perfekt, aber zur Not geht’s damit auch). Die erste Messung zerstört die zweite Messgröße, d.h. man bekommt dann zwar einen Wert, aber das ist nicht mehr der, den man wissen wollte. Die Messungen sind „nicht kommutativ“ (lat. commutare = vertauschen). Ihr seid es natürlich gewohnt, dass 3 + 5 das Gleiche ist wie 5 + 3. Wäre es anders, müsste man ja im Supermarkt genau darüber nachdenken, in welcher Reihenfolge man die Waren aufs Kassenband legt, damit der Einkauf nicht zu teuer wird.

Quantenmessungen sind aber Matrizen. Die senkrechte Polarisation misst man mit

Senkrecht polarisiertes Licht wird dadurch nicht verändert:

Man sagt, |s ist ein „Eigenzustand“ von S. Man kann ein Polarisationsfilter auch schräg einstellen, sodass das Licht |v unverändert passieren kann. Nennen wir den zugehörigen Operator V, so wäre

V |v = |v .

Ich erspare euch die Rechnung. Nur für den unwahrscheinlichen Fall, dass doch jemand nachrechnen möchte: Es ist

Misst man erst mit V und dann mit S (man schreibt die Operatoren von rechts nach links, also was direkt an |v steht, wird zuerst auf |v angewendet), so würde man rechnen S V |v und erhielte

S V |v= 0,6 · |s.

Misst man erst mit S und dann mit V, so folgt:

V S |v= 0,36 · |v .

Kurz und gut, V S ist etwas Anderes als S V. Die Differenz S V – V S ist also nicht 0. Ist ja auch logisch; wenn man erst mit V und dann mit S misst, erhält man am Ende Licht in Richtung von |s, da aus einem senkrechten Polarisationsfilter nun mal senkrecht polarisiertes Licht rauskommt. Misst man dagegen erst mit S und dann mit V, dann erhält man am Ende Licht in Richtung von |v.

Quanten-Nerds kürzen S V – V S mit [S,V] ab und nennen es den „Kommutator von S und V“. Mittels Matrixmultiplikation kann man [S,V] direkt ausrechnen (muss man aber nicht):

Wenn der Kommutator zweier Operatoren nicht 0 ist, so wie hier, dann sind die beiden zugehörigen Observablen nicht simultan messbar. Ist hingegen der Kommutator 0, dann ist die Reihenfolge der Messungen egal, die Observablen sind simultan messbar. Ein Beispiel: Der Operator

winkt jedes Lichtquant durch und misst daher eigentlich nur dessen Anwesenheit. Für den Kommutator mit S erhält man:

Man kann also I und S in beliebiger Reihenfolge anwenden, die eine Messung stört die andere nicht. In der „richtigen“ Quantenphysik formulierte Max Born eine Variante von Heisenbergs Unbestimmtheitsrelation als [p,q] = pq – qp  0. Hey, das steht sogar im PR-Report in Heft 3334. (Da steht sogar, was statt dessen rauskommt, nämlich h/2i, aber das muss euch nicht belasten.) In Worten: Impuls und Ort kann man nicht simultan messen.

Wenn ihr euch noch mal Bild 1 anseht, bekommt ihr eine Ahnung, was das bedeutet. Der Ort des Quantenobjektes ist irgendwo da, wo ||² nennenswert von 0 abweicht, denn das ist ja die Wahrscheinlichkeit, das Ding dort zu treffen. Die Frequenz f (Schwingungen pro Sekunde) der Schwingung von  hängt mit dem Impuls p zusammen, bei Licht ist er zum Beispiel p = f · h/c, Frequenz mal Planck-Konstante durch Lichtgeschwindigkeit. Nun kann man bei einem so komprimierten Wellenpaket wie in Bild 1 schlecht die Schwingungen pro Sekunde zählen. Das ist, wie wenn ihr eure Pulsfrequenz (Schläge pro Minute) zählen wollt. Eine Sekunde lang zählen und das Ergebnis mal 60 nehmen wird bestimmt keine Präzisionsmessung. 15 Sekunden zählen und dann mal 4 wird schon genauer. Noch besser zählt man eine Minute lang. Ebenso wird bei dem kurzen Wellenpaket die Frequenzmessung (= Impulsmessung) ungenau. Um sie genauer zu machen, müsste das Wellenpaket länger sein. Dann aber zieht sich auch ||² in die Länge und die Ortsbestimmung wird ungenauer. Beides zugleich kann man nicht haben.

Der Kollaps der Zustandsfunktion

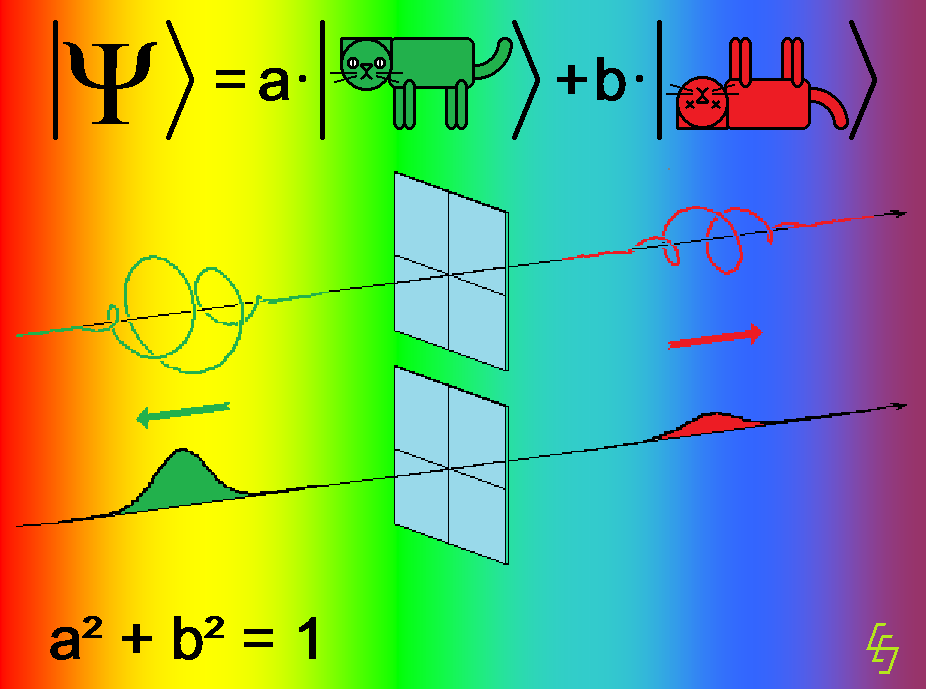
Durch einen Kalkspat-Kristall (chemisch Kalziumkarbonat CaCO₃) hindurch sieht man ein Doppelbild, der Effekt heißt daher Doppelbrechung (Bild 3 links). Ein Lichtstrahl wird in dem Kristall (KS) in einen „ordentlichen“ Strahl o (im Bild mit waagerechter Polarisation) und einen „außerordentlichen“ Strahl a (mit senkrechter Polarisation) aufgespalten (Bild 3 rechts).

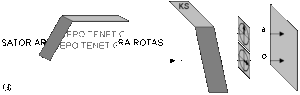
Ein Lichtquant des Zustandes |w kommt dann hinter dem Kristall bei o heraus und hinterlässt eine Schwärzung unten auf der Fotoplatte (die im Bild ganz rechts steht). Ein Lichtquant des Zustandes |s kommt bei a heraus und hinterlässt eine Schwärzung oben auf der Fotoplatte. Da der Kristall nur diese beiden Zustände produzieren kann, sind sie seine Eigenzustände.

Er wirkt im oberen Weg wie ein senkrechtes Polarisationsfilter

und im unteren wie ein waagerechtes Polarisationsfilter

Wie aber, wenn ein einzelnes Lichtquant des Zustandes |v in den Kristall eintritt? Jetzt wird es spannend. Man erinnert sich, dass

|v = 0,8 · |w + 0,6 · |s

war. Hinter dem Kristall müsste der Anteil 0,8 · |w unten und der Anteil 0,6 · |s oben herauskommen. Das Lichtquant kann sich aber nicht aufteilen, es muss entweder oben oder unten in die Fotoplatte einschlagen. Die Aussage der Quantenphysik ist, dass es mit der Wahrscheinlichkeit (glauben oder nachrechnen  !)

(also 64 %) unten auf die Platte trifft, und mit

(also 36 %) oben. Dass 0,64 + 0,36 = 1 ist, spiegelt die Tatsache wider, dass das Quant nicht verloren geht. Die Summe der Wahrscheinlichkeiten, es irgendwo wiederzufinden, ist 1 oder 100 %. Der Kristall erzeugt also aus einem beliebigen Zustand einen seiner Eigenzustände. Der Übergang vom Zustand |v in einen der Zustände |w oder |s ist der schon erwähnte „Kollaps der Zustandsfunktion“. Er findet irgendwie außerhalb der Quantenphysik statt, denn diese ist deterministisch, während der Kollaps probabilistisch (= zufallsbestimmt) ist. Die Quantenphysik lässt sich an keiner Stelle darüber aus,

– wo das passiert,

– wie das passiert,

– ob es überhaupt passiert.

Ein zusätzliches Element scheint erforderlich zu sein, das nicht Bestandteil der Quantenphysik ist. Darum geht es in der nächsten Folge. Ach ja, und noch ’ne Warnung: Ich entfalte euch hier meine persönliche Sichtweise. Gerade, wo es ans Interpretieren geht, endet die Objektivität. Und ich werde viel interpretieren.